POLÍGONO.- Es una porción de plano limitada por una curva cerrada llamada “línea poligonal”.
POLÍGONO CONVEXO.- Aquellos que tienen su línea poligonal respecto a una curva exterior.
POLIGONO CÓNCAVO.- Esta formado por una línea cóncava que tiende a una curvatura hacia adentro.
Video relativo a la clasificación de polígonos.
POLÍGONO REGULAR.- Es el que tiene todos sus lados y todos sus ángulos iguales, es equilátero y es equiángulo.
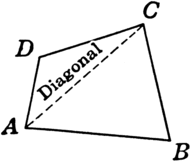
DIAGONAL.- Segmento determinado por dos vértices no consecutivos.
CENTRO.- Se refiere al punto central de las circunferencias circunscrita e inscrita en polígonos regulares.
RADIO.- Segmento que une el centro del polígono con un vértice, es también el radio de la circunferencia circunscrita.
APOTEMA.- Segmento que une el centro del polígono perpendicularmente con cualquier lado, es también el radio de la circunferencia inscrita.
ÁNGULO CENTRAL.- Es el ángulo formado por los radios correspondientes (dos vértices consecutivos).
“FÓRMULAS SOBRE TEOREMAS DE POLÍGONOS”.✿ Teorema No. 1. La suma de los ángulos interiores de un polígono es igual a 180° (n-2), donde “n” es el lado, o mejor, el número de lados del polígono.
• Calcular la suma de los ángulos interiores de un pentágono regular.Suma de ángulos interiores = 180(n-2)Suma de ángulos interiores = 180(5-2)Suma de ángulos interiores = 180(3)Suma de ángulos interiores = 540°.
✿ Teorema No. 2. Si se quiere calcular el ángulo interior de algún polígono, éste debe ser regular, el valor de cada uno de sus ángulos es el mismo y es igual a la división de la suma de los ángulos interiores entre “n”.Ángulo interior = 180(n-2)n
EJEMPLO:• Calcular el ángulo interior de un pentadecágono (15 lados) regular.
Ángulo interior = 180(n-2) = 180(15-2) = 180(13) = 2340 = 156°n 15 15 15
✿ Teorema No. 3. La suma de los ángulos exteriores de un polígono es de 360°.
Ángulo exterior = 360°n
EJEMPLO:• Calcular el ángulo exterior de un triángulo.
Ángulo exterior = 360° = 360° = 120°n 3
✿ Teorema No. 4. El número de diagonales que pueden trazarse desde los vértices de un polígono es igual al producto de n(n-3) y todo ello dividido entre 2.
# de / = n(n-3)2
EJEMPLO:• Calcular el número de diagonales de un pentágono regular.
# de / = n(n-3) = 5(5-3) = 5(2)= 10 = 5 diagonales.2 2 2 2
En la siguiente página web, te mostramos algunos ejercicios que puedes tomar en cuenta para repasar tu clase de matemáticas:
Esperamos que nuestro blog, te haya sido útil...
¡GRACIAS!
Deja tus comentarios.