POLIGONOS. Conceptos y teoremas.

POLÍGONO.- Es una porción de plano limitada por una curva cerrada llamada “línea poligonal”.

POLÍGONO CONVEXO.- Aquellos que tienen su línea poligonal respecto a una curva exterior.

POLIGONO CÓNCAVO.- Esta formado por una línea cóncava que tiende a una curvatura hacia adentro.

Video relativo a la clasificación de polígonos.

POLÍGONO REGULAR.- Es el que tiene todos sus lados y todos sus ángulos iguales, es equilátero y es equiángulo.

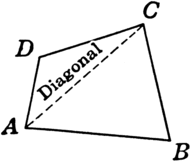
DIAGONAL.- Segmento determinado por dos vértices no consecutivos.

CENTRO.- Se refiere al punto central de las circunferencias circunscrita e inscrita en polígonos regulares.

RADIO.- Segmento que une el centro del polígono con un vértice, es también el radio de la circunferencia circunscrita.

APOTEMA.- Segmento que une el centro del polígono perpendicularmente con cualquier lado, es también el radio de la circunferencia inscrita.

ÁNGULO CENTRAL.- Es el ángulo formado por los radios correspondientes (dos vértices consecutivos).

“FÓRMULAS SOBRE TEOREMAS DE POLÍGONOS”.
✿ Teorema No. 1. La suma de los ángulos interiores de un polígono es igual a 180° (n-2), donde “n” es el lado, o mejor, el número de lados del polígono.

EJEMPLO:
• Calcular la suma de los ángulos interiores de un pentágono regular.
Suma de ángulos interiores    = 180(n-2)
Suma de ángulos interiores      = 180(5-2)
Suma de ángulos interiores      = 180(3)
Suma de ángulos interiores      = 540°.

✿ Teorema No. 2. Si se quiere calcular el ángulo interior de algún polígono, éste debe ser regular, el valor de cada uno de sus ángulos es el mismo y es igual a la división de la suma de los ángulos interiores entre “n”.
Ángulo interior = 180(n-2)
                               n

EJEMPLO:
• Calcular el ángulo interior de un pentadecágono (15 lados) regular.

Ángulo interior = 180(n-2) = 180(15-2) = 180(13) = 2340 = 156°
                                 n                15             15           15

✿ Teorema No. 3. La suma de los ángulos exteriores de un polígono es de 360°.

Ángulo exterior = 360°
                                 n

EJEMPLO:
• Calcular el ángulo exterior de un triángulo.

Ángulo exterior = 360° = 360° = 120°
n 3

✿ Teorema No. 4. El número de diagonales que pueden trazarse desde los vértices de un polígono es igual al producto de n(n-3) y todo ello dividido entre 2.

# de / = n(n-3)
2